Manual

"Smoking is one of the leading causes for statistics..."

Monte Carlo Statistics:

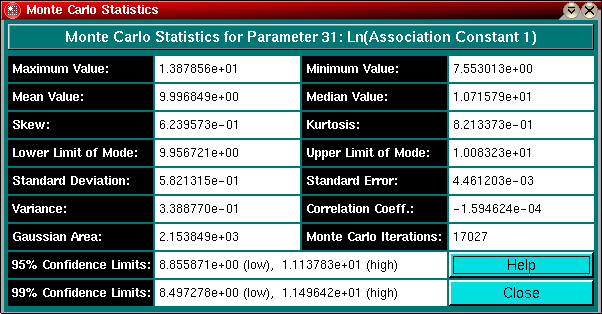
This panel shows the various statistical measurements for the Monte Carlo distributions of each parameter.

Explanation of Fields:

Variables used: u is the mean data value (see below), N refers to the number of observations, and x_i is the observation i.

• Maximum and Minimum Value:
  The maximum and minimum value occuring in the distribution for the parameter. The closer these values are together, the smaller the spread of values and the more reliable is the mean.

• Mean Value:
  The mean is the average value of all measurements:
  

• Median Value:
  After sorting the data from lowest to highest, the median is the 'middle' value or the 50th Percentile, meaning that 50% of the results from the simulation are less than the median. If there is an even number of data points, then the median is the average of the middle two points.

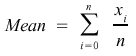
  Extreme values can have a large impact on the mean, so the median is often preferrable for skewed distributions such as the Lognormal distribution. If the distribution is symmetric (like the Normal distribution), then the mean and median will be identical."

  The key is that last sentence. IF the distribution is symmetric, then the median will happen to be the same as (Max+Min)/2 in addition to the mean. But that is generally not the case for Monte Carlo simulations. The values of Min and Max can vary dramatically (even when the distribution is symmetric), but the median does not depend upon the minimum and maximum values, only the middle point.

  This value should be close to the mean and the mode, if not, the distribution may be skewed.

• Skew and Kurtosis:
  The skew and kurtosis measure how the values are distributed around the mode (see below). A skew value of zero indicates that the values are evenly distributed on both sides of the mode. A negative skew indicates an uneven distribution with a higher than normal distribution of values to the right of the mode, a positive value for the skew indicates a larger than normal distribution of values to the left of the mode. The kurtosis of the distribution indicates how narrow or broad the distribution is. A positive value for the kurtosis indicates a narrower distribution than a normal Gaussian, a negative value indicates a flatter and broader distribution. A normal Gaussian distribution has a kurtosis of zero. The larger the kurtosis of the parameter, the better.
  
  
  
  

• The Mode:
  The mode is the value in the distribution that occurs most frequently. Since floating point values rarely repeat, values are collected in bins of finite size for comparison. The lower limit of the mode refers to the lower limit of the bin that has the largest frequency. The upper limit of the mode is the value of the largest parameter value to still be counted in this bin. In a normal distribution the mean = mode = median. The larger the difference between these values, the more the distribution deviates from a normal Gaussian.

• Variance:
  The variance is the sum of squares of the deviations from the mean, normalized by the number of datapoints. It is given by the expression
  

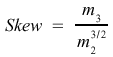
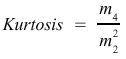
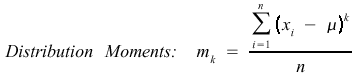
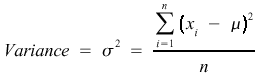
  A smaller variance is better.

• Standard Deviation:
  The standard deviation , commonly denoted by sigma, is the square root of the variance
  

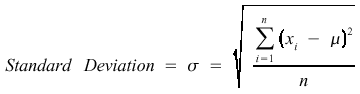
  This is a standard measure of the spread in data values. The larger the value of sigma, the larger is the spread in data. If data are normally distributed, sigma as calculated by Eq.(5) can be substituted in Eq.(1) to find the probability for a particular data value. The smaller the standard deviation, the higher is the confidence in the estimated value.

• Standard Error:
  The standard error is equal to the standard deviation devided by the the square-root of the number of observations.

• Correlation Coefficient:
  The correlation coefficient is a measure of how correlated the datapoints are in the fit. A random distribution should have very little correlation. A good value here should be around zero.

• Gaussian Area:
  The Gaussian area is the area under the curve described by the bin, or the distribution of values.

• Monte Carlo Iterations:
  This is the number of curvefits that were performed in the Monte Carlo Analysis. It is equivalent to the number of observations for each parameter.

• 95% and 99% Confidence Intervals:
  The confidence intervals identify the probability limits of a range between which the true value of the parameter is to be expected with a given likelyhood. In statistics, rather than talk about the `answer', one gives the mean and a set of upper and lower limits. For random errors, the limits give the range of values within which the actual answer is likely to fall to some level of confidence. For example, the limits for a 90% confidence level give the range of values where we have a nine in ten chance that the actual answer lies.

  For real variations in properties between multiple samples, the limits specify a range in which it is likely to measure some percentage of data values. For example, one can specify limits so that one nine of every ten measurements are likely to fall within the range of values between those limits; this would be a 90% confidence level. A 99% confidence level, where on average 99 out of 100 measurements would be found, would require larger confidence limits. To be sure that each measurement fell within some range of values (a 100% confidence level) would require limits of plus and minus infinity; in other words statistically you can never be 100% sure of your answer or possible range of data values!

  Obtaining confidence limits depends on the data distribution. For a normal probability these limits are reasonably straight-forward to obtain. If the kurtosis and skew of the distribution are close to zero, the distribution is similar to a normal distribution and the confidence limits represent a good measure of the error range. For example, say we have a normal distribution with some mean u and a standard deviation of sigma. The probability of measuring a data value between 2 x sigma and 3 x sigma would be

  

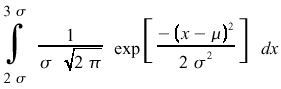
  The limits for a particular confidence level for a normal distribution are simply the limits of integration on either side of the mean needed so that the integral covers the desired area. For example, for a 95% confidence level we need to find the upper and lower limits so that 95% of the area under the curve falls between these two points. The equation for this is

  

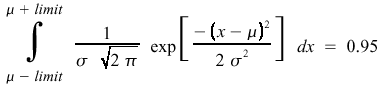
  where +/-limit are referred to as the confidence limits, measured in standard deviations. The desired confidence limit in percentage can be looked up in tables, for a 95% confidence interval, the limit should be about 1.96 standard deviations around the mean, for a 99% interval the limit should be about 2.576 standard deviations around the mean.

For more information see also:

Wittwer, J.W., "Monte Carlo Simulation in Excel: A Practical Guide" From Vertex42.com, June 1, 2004, http://vertex42.com/ExcelArticles/mc/